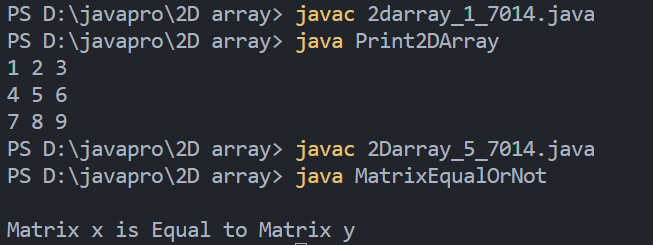
1. Enter the Matrix of rows and columns entered by the user and print in matrix format
class Print2DArray {
public static void main(String[] args) {
final int[][] matrix = {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
for (int i = 0; i < matrix.length; i++)
{
for (int j = 0; j < matrix[i].length; j++)
{
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}
Output
2. Program to Add Two Matrices
class MatrixAddition{
public static void main(String args[]){
int arr1[][]={{15,3,4},{5,4,3},{3,4,5}};
int arr2[][]={{1,8,4},{2,4,3},{1,2,4}};
int arr3[][]=new int[3][3];
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
arr3[i][j]=arr1[i][j]+arr2[i][j];
}
}
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
System.out.print(arr3[i][j]+" ");
}
System.out.print("\n");
}
}
}
Output
3. Program to Multiply Two Matrices
/*Program to Multiply Two Matrices*/
class MatrixMultiplication{
public static void main(String args[]){
int a[][]={{1,1,1},{2,2,2},{3,3,3}};
int b[][]={{1,1,1},{2,2,2},{3,3,3}};
int c[][]=new int[3][3];
//multiplying and printing multiplication of 2 matrices
for(int i=0;i<3;i++){
for(int j=0;j<3;j++){
c[i][j]=0;
for(int k=0;k<3;k++)
{
c[i][j]+=a[i][k]*b[k][j];
}//end of k loop
System.out.print(c[i][j]+" "); //printing matrix element
}//end of j loop
System.out.println();//new line
}
}}
Output
4. Program to subtract the two matrices
import java.util.Scanner;
class MatrixSubtraction {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
System.out.print("Enter the number of rows: ");
int rows = input.nextInt();
System.out.print("Enter the number of columns: ");
int columns = input.nextInt();
int[][] matrix1 = new int[rows][columns];
int[][] matrix2 = new int[rows][columns];
int[][] result = new int[rows][columns];
// Input for the first matrix
System.out.println("Enter elements of the first matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
matrix1[i][j] = input.nextInt();
}
}
// Input for the second matrix
System.out.println("Enter elements of the second matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
matrix2[i][j] = input.nextInt();
}
}
// Subtract the matrices
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
result[i][j] = matrix1[i][j] - matrix2[i][j];
}
}
// Display the result
System.out.println("Result of matrix subtraction:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
System.out.print(result[i][j] + " ");
}
System.out.println();
}
input.close();
}
}
Output
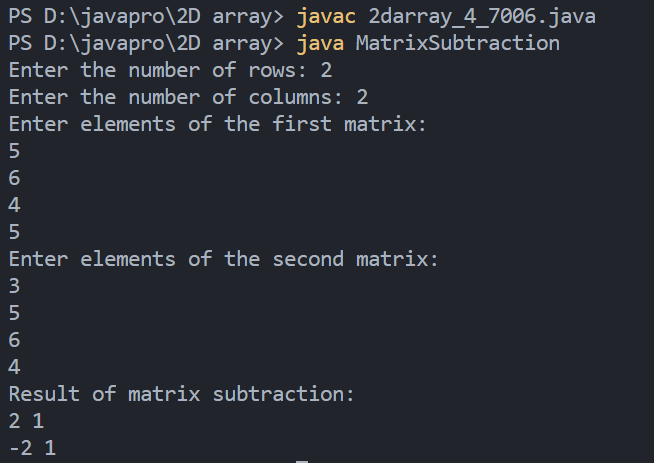
5. Program to determine whether two matrices are equal
class MatrixEqualOrNot {
public static void main(String[] args) {
int[][] x = {{1, 2}, {3, 4}};
int[][] y = {{1, 2}, {3, 4}};
int i, j, isEqual = 1;
for(i = 0; i < x.length; i++)
{
for(j = 0; j < x[0].length; j++)
{
if(x[i][j] != y[i][j]) {
isEqual = 0;
break;
}
}
}
if(isEqual == 1) {
System.out.println("\nMatrix x is Equal to Matrix y");
}
else {
System.out.println("\nMatrix x is Not Equal to Matrix y");
}
}
}
Output
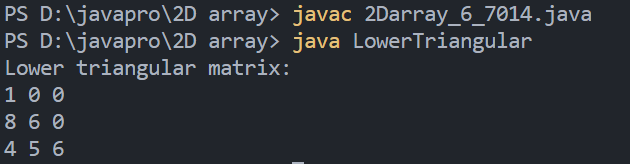
6. Program to display the lower triangular matrix
class LowerTriangular
{
public static void main(String[] args) {
int rows, cols;
int a[][] = {
{1, 2, 3},
{8, 6, 4},
{4, 5, 6}
};
rows = a.length;
cols = a[0].length;
if(rows != cols){
System.out.println("Matrix should be a square matrix");
}
else {
System.out.println("Lower triangular matrix: ");
for(int i = 0; i < rows; i++){
for(int j = 0; j < cols; j++){
if(j > i)
System.out.print("0 ");
else
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
}
}
Output
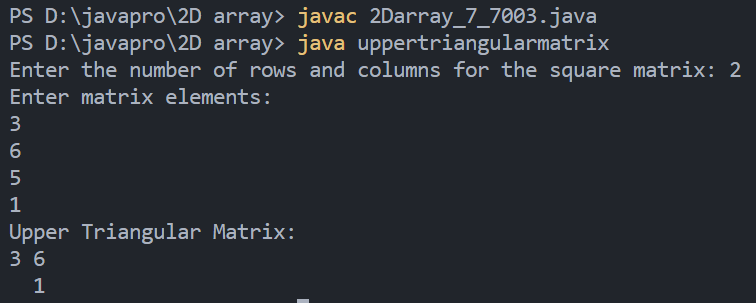
7. Program to display the upper triangular matrix
import java.util.Scanner;
class uppertriangularmatrix {
public static void main(String[] a) {
Scanner s = new Scanner(System.in);
System.out.print("Enter the number of rows and columns for the square matrix: ");
int n = s.nextInt();
int[][] matrix = new int[n][n];
System.out.println("Enter matrix elements:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = s.nextInt();
}
}
System.out.println("Upper Triangular Matrix:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (j >= i) {
System.out.print(matrix[i][j] + " ");
} else {
System.out.print(" ");
}
}
System.out.println(" ");
}
}
}
Output
9. Program to find the sum of each row and each column of a matrix
class ary2 {
public static void main(String[] args) {
int[][] matrix = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
int rows = matrix.length;
int columns = matrix[0].length;
int[] rowSums = new int[rows];
int[] columnSums = new int[columns];
// Calculate row sums
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
rowSums[i] += matrix[i][j];
}
}
// Calculate column sums
for (int j = 0; j < columns; j++) {
for (int i = 0; i < rows; i++) {
columnSums[j] += matrix[i][j];
}
}
// Print row sums
System.out.println("Sum of each row:");
for (int i = 0; i < rows; i++) {
System.out.println("Row " + (i + 1) + ": " + rowSums[i]);
}
// Print column sums
System.out.println("\nSum of each column:");
for (int j = 0; j < columns; j++) {
System.out.println("Column " + (j + 1) + ": " + columnSums[j]);
}
}
}
Output
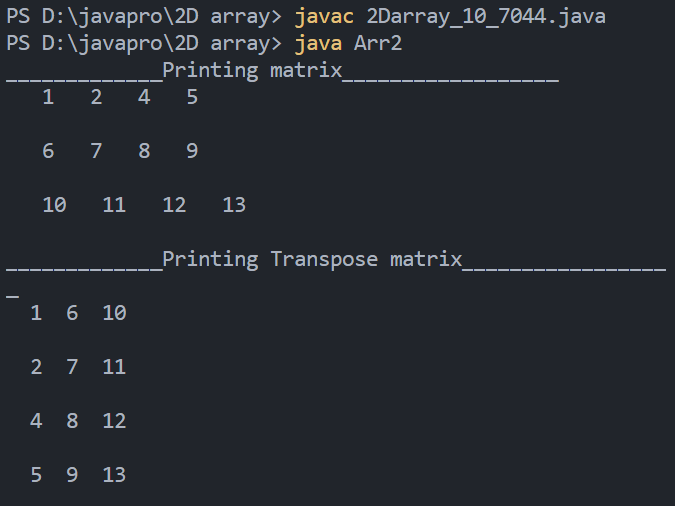
10. Program to find the transpose of a given matrix
class Arr2 {
public static void main(String[] args) {
int a[][] = {
{ 1, 2, 4, 5 },
{ 6, 7, 8, 9 },
{ 10, 11, 12, 13 }
};
int rows = a.length;
int columns = a[0].length;
int transpose[][] = new int[columns][rows];
System.out.println("_____________Printing matrix__________________");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
System.out.print(" " + a[i][j]);
transpose[j][i] = a[i][j];
}
System.out.println("\n");
}
System.out.println("_____________Printing Transpose matrix__________________");
for (int i = 0; i < columns; i++) {
for (int j = 0; j < rows; j++) {
System.out.print(" " + transpose[i][j]);
}
System.out.println("\n");
}
}
}
Output
11. Program to determine whether a given matrix is an identity matrix
class Identity
{
public static void main(String[] args) {
int rows, cols;
boolean flag = true;
int a[][] = {
{1, 0, 0},
{0, 1, 0},
{0, 0, 1}
};
rows = a.length;
cols = a[0].length;
if(rows != cols){
System.out.println("Matrix should be a square matrix");
}
else {
for(int i = 0; i < rows; i++){
for(int j = 0; j < cols; j++){
if(i == j && a[i][j] != 1){
flag = false;
break;
}
if(i != j && a[i][j] != 0){
flag = false;
break;
}
}
}
if(flag)
System.out.println("Given matrix is an identity matrix");
else
System.out.println("Given matrix is not an identity matrix");
}
}
}
Output

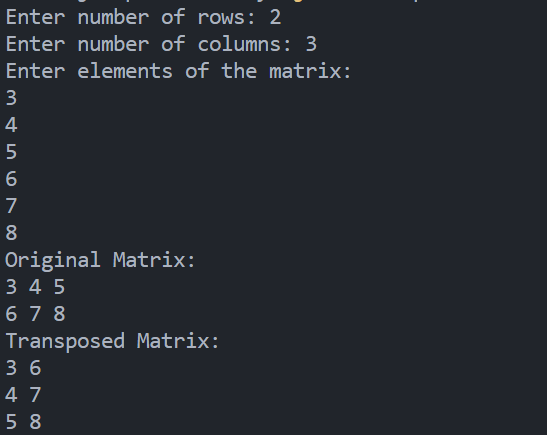
12. Program to Transpose matrix
import java.util.Scanner;
class transposematrix {
public static void main(String[] a) {
Scanner s = new Scanner(System.in);
System.out.print("Enter number of rows: ");
int rows = s.nextInt();
System.out.print("Enter number of columns: ");
int columns = s.nextInt();
int[][] matrix = new int[rows][columns];
System.out.println("Enter elements of the matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
matrix[i][j] = s.nextInt();
}
}
int[][] transpose = new int[columns][rows];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
transpose[j][i] = matrix[i][j];
}
}
System.out.println("Original Matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
System.out.println("Transposed Matrix:");
for (int i = 0; i < columns; i++) {
for (int j = 0; j < rows; j++) {
System.out.print(transpose[i][j] + " ");
}
System.out.println();
}
}
}
Output
